In dit onderdeel zie je hoe een goniometrische grafiek uit een cirkel met straal 1 ontstaat.
In een rechthoekige driehoek zijn de sinus, cosinus en tangens beperkt tot scherpe hoeken. In een cirkel echter kun je verder draaien dan 90 graden. De grootte van de draaihoek past bij de lengte van de cirkelboog.
Een cirkel met straal 1 heet eenheidscirkel en heeft een omtrek van 2
. In die cirkel geldt bijvoorbeeld:
-draaihoek 90 graden past bij kwartcirkel met lengte ½=1,57…
-draaihoek 60 graden past bij cirkelboog met lengte 1/3=1,04…
Het is handig om voor de hoek dezelfde getalswaarde te nemen als die van de booglengte. Die hoekmaat heet radiaal. Zo is een rechte hoek 0,5 radialen.
Je kunt de hoek automatisch laten draaien of met behulp van een handje. Bij het draaien van de hoek loopt een rood punt over de cirkel. In de grafiek is de horizontale variabele de draaihoek. De horizontale afstand is de booglengte.
sinus
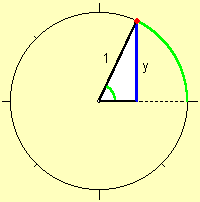
In een rechthoekige driehoek geldt: 
In de eenheidscirkel wordt dit: 
Dit is de verticale variabele in de grafiek.
cosinus
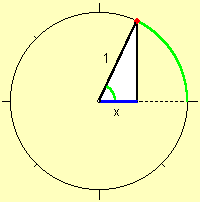
In een rechthoekige driehoek geldt: 
In de eenheidscirkel wordt dit: 
Dit is de verticale variabele in de grafiek.
tangens
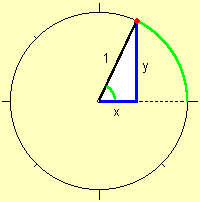
In een rechthoekige driehoek geldt:
In de eenheidscirkel wordt dit: 
Dit is de verticale variabele in de grafiek.
Buttons
Met deze balk regel je de animatie.