In het venster voor voorschrift-invoer kun je een voorschrift invoeren , een bestand openen maar ook het format van de tekening regelen.
3D figuren
De 3D figuur kun je zien als gebouwd op een draadmodel. Het draadmodel bestaat uit polygonen die liggen in vlakken loodrecht op de x-as en de y-as. Hoe meer stappen langs de assen hoe fijner het model en hoe fraaier de grafiek, maar ook hoe langer het duurt voordat de tekening klaar is.
In de tekening is het draadmodel zichtbaar te maken met de knoppen X=constant,en Y=constant.
De punten worden getekend volgens het voorschrift z=f(x,y)
Op het tekenscherm kun je met twee schuiven de kijkrichting manipuleren.
Het beeld van de 3D figuur hangt af van de manier waarop je er tegen aan kijkt. Je stelt dat in met twee hoeken, θ en φ
θ is de hoek die het oog maakt met de verticale z-as. φ is de hoek in het XOY-vlak tussen de x-as en de schaduw van de kijk-rechte.
Je kunt je het veranderen van de hoeken als volgt voorstellen: Als θ gelijk is aan 0 graden, dan kijk je loodrecht naar omlaag. Als θ groter wordt beweegt de kijkrechte naar omlaag. Als θ=90 graden dan kijk je horizontaal en als θ nog groter wordt kijk je van onderen tegen de grafiek aan. Het veranderen van φ houdt in dat je blikrichting om de verticale as draait. Een toename van 180 graden komt er dus op neer dat je de figuur van de andere kant bekijkt.
Je kunt zowel de 3D grafiek als de niveaulijnen tekenen, afzonderlijk of tegelijk.
Bij het tekenen van de 3D grafiek wordt achteraan begonnen, waarbij stukken die meer naar voren liggen over de achterliggende stukken heen worden getekend, naarmate het werk vordert.
Met X=Constant en Y=Constant kun je kiezen of het draadmodel al of niet op het oppervlak worden getekend.
Met behulp van de trace knop zie je het verband tussen het 3-D beeld van de grafiek en de niveaulijnen
De optie Assen geeft de mogelijkheid de assen al of niet zichtbaar te laten tekenen.
De optie Gevuld maakt het oppervlak gekleurd of niet.
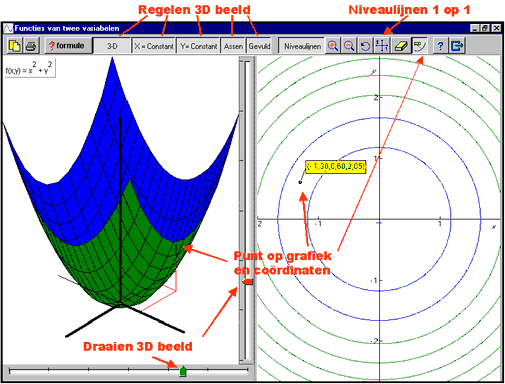
De tekenwijze
De figuur op het scherm wordt getekend alsof het oog zich in het oneindige bevindt. Verder bestaat ertussen het punt (x,y,z) in de ruimte en het punt (X,Y) op het scherm het volgende verband: X = -xsinφ + ycosθ Y = -xcosθcosφ - ycosθsinφ + zsinθ
Behalve de ruimtelijke voorstelling van het oppervlak z=f(x,y) kun je ook niveaulijnen in het XOY-vlak tekenen.
Voordat de niveaulijnen worden getekend berekent het programma eerst de waarden van de functie binnen een rechthoekig rooster van horizontale en verticale lijnen. De niveaulijnen worden berekend door de originele functie f te benaderen door een bilineaire functie
H(x,y)=a +bx+cy+dxy. De waarden van a, b, c en d worden bepaald door de functiewaarden in de vier hoekpunten. Als de vier hoekpunten van de rechthoek gelijk waren aan (0,0), (x,0), (0,y) en (x,y) dan zou de bilineaire functie H(x,y) bepaald zijn door
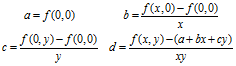
Zo is binnen elk klein rechthoekje het probleem terug gebracht tot het vinden van niveaulijnen van de bilineaire functie H(x,y), die de vorm van een hyperbool of van ontaarde hyperbolen hebben. Mocht de functie niet bestaan in een hoekpunt, dan wordt er in dat rechthoekje niets getekend.