Polynomen zijn de meest eenvoudige functies die je in de analyse tegen komt. Je kunt er aangenaam meewerken wanneer er numeriek gerekend moet worden, want hun functiewaarden kunnen gevonden worden na het uitvoeren van een eindig aantal vermenigvuldigingen en optellingen. Met deze optie kan worden gedemonstreerd dat veel functies, zoals exponentiële en goniometrische, kunnen worden benaderd door polynomen.
Als een functie voor zekere waarde van x afgeleiden heeft van de graad n, dan is de Taylor polynoom van de n-de orde gedefinieerd als
![]()
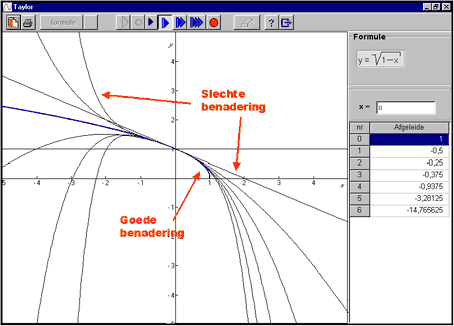
Niet altijd geven Taylor polynomen een goede benadering van een functie.
Zo is bijvoorbeeld de Taylor benadering van de functie f(x) = √(1-x) voor x=0, alleen maar een redelijke in het interval (-1,1).
De functie bestaat niet voor x>1 en voor x<-1 verschilt de functie sterk van de benadering.
De figuur laat ook het interessante verschijnsel zien van het symmetrische convergentiegebied van een machtreeks.
Je kunt zien dat de machtreeks in de buurt van het convergentiegebied een slechte benadering kan zijn.