Detta verktyg används främst för att lösa ekvationer av typen f(x) = 0.
Rita Graf kan man naturligtvis rita funktionen och sedan zooma in mot funktionens nollställe. Här finns ett verktyg med iterativa metoder och då måste vi först skriva om på formen f(x) = x.
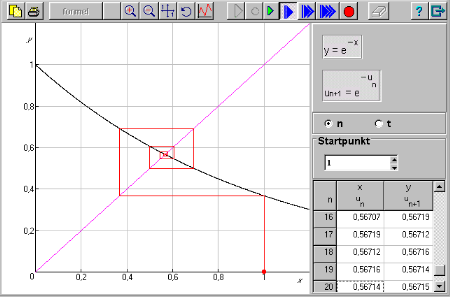
Sedan gäller det att hitta en bra startpunkt för den iterativa processen. I vårt exempel kan vi t.ex. starta vi med värdet 1.och vi matar in detta värde i inmatningsrutan. Nu kan vi starta vår process genom att klicka på någon av tempoknapparna.
Efter cirka 20 iterationer blir de första fyra decimalerna stabila.
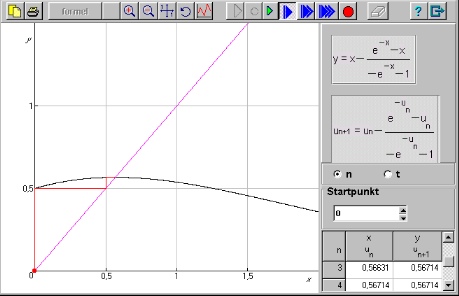
En mer effektiv metod som kräver betydligt mindre antal iterationer för att lösa ekvationer numeriskt med ett iterativt förfarande är Newton-Raphsons metod. Den brukar beskrivas i läroböcker. Då skriver man funktionen i vårt exempel som och formeln för Newton Raphsons metod brukar skrivas
Man använder här alltså derivatan av funktionen. Vi ser att vi får stabila värden efter tre iterationer.
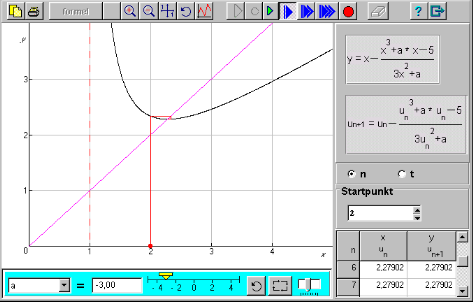
Relationer som innehåller parametrar kan också studeras. Antag att vi vill beräkna rötterna till ekvationen
för olika värden på a. Då skriver vi i vår funktion i parameterform och ställer in intervallet för parametervärdet. Tabellen och grafen uppdateras när vi drar i parameterslitsen längst ner.
För att ange att det är en rekursiv formel du arbetar med så används i beteckningarna: 
visar också en s.k. tidsgraf med med n eller t på den horisontella axeln.
När värdet på n eller t ökas så ändras den horisontella axeln automatiskt. Detta gör att iterativa processer blir lätta att följa.
Det finns alltså tre sätt som iterationer kan studeras på:
spindelnätsdiagram
tidsgraf
tabell