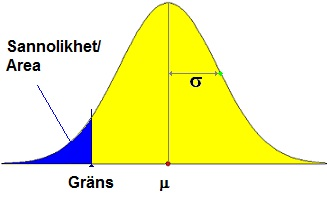
Normalfördelningen bestäms av två parametrar, medelvärdet µ (uttalas my) och standardavvikelsen s (sigma). Ett typexempel på normalfördelningen är längderna hos en stor grupp människor av samma kön och hur längderna fördelar sig kring medelvärdet.
Normalfördelningens så kallade frekvensfunktion är kontinuerlig, symmetrisk runt medelvärdet och unimodal, dvs. har endast en topp.
Om fördelningen har parametrarna µ = 0 och s = 1 talar man om den standardiserade normalfördelningen, vilket är utgångsvärdet på skärmen. Du kan dock ändra µ till ett godtyckligt värde och s till ett godtyckligt positivt värde, varvid x-axeln ändras automatiskt om du har klickat i rutan ”anpassa figuren”.
Du kan dra i gränserna mellan det gula och blå området.
Du kan ändra värden på µ genom att skriva i rutan eller dra i den lilla röda cirkeln.
Du kan ändra värden på s genom att skriva i rutan eller dra i den lilla gröna symbolen.
Grafens tolkning är P(X<=gräns|µ; s) = sannolikheten motsvarande den blå ytan.
Når du använder denna modul för att göra en beräkning, tänk på att det finns fyra parametrar: gräns(er), sannolikhet/area, µ och s.
| • | µ och s bestämmer grafens utseende. |
| • | Till en gräns hör en area/sannolikhet och vice versa. |
Det finns ett samband mellan dessa fyra parametrar. Du kan upptäcka detta om du ändrar/drar i någon av dessa parametrar.
Värdet på en av dessa parametrar kan beräknas om du känner till värdena på de andra tre. Se uppställningen nedan:
Area/Sannolikhet söks ange µ, s och gräns(er)
Gräns(er) söks ange µ, s och area
µ söks ange s, area och gräns(er)
s söks ange µ, area och gräns(er)
Under Sök parameter kan du göra ditt val.
Det finns några olika visningsmöjligheter:
Anpassa figuren
Detta val anpassar skalningen på axlarna och kurvan ritas i mitten.
z-axel
En andra horisontell axel visar den standardiserade normalfördelningen (med µ = 0 och s = 1) som man får genom att räkna om den aktuella stokastiska variabeln enligt formeln (X - µ)/s.
Lådagram
Man kan också få ett lådagram utritat på skärmen.